In this unit, we learned about rearranging an equation in standard form to slope y- intercept form, rearranging an equation in slope y-intercept form to standard form, angle relationships in triangles, quadrilaterals, and polygons, how to find the midpoints and medians in triangles and quadrilaterals, graphing using x and y intercepts, parallel and perpendicular lines, and finding equations of lines given the slope and a point.

First, we learned about rearranging an equation in standard form to slope y-intercept form.
It is more useful to write an equation in slope y-intercept form, since slope y-intercept has more info, and it easier to graph.

To rearrange a standard form equation to a slope y-intercept, we isolate the y-term on one side of the equation, so it looks like: y= mx + b.

EXAMPLE: Ax + By + C = 0
                     By = -Ax - C
If the coefficient is something like '3y', then divide each term by the coefficient next to y.
EXAMPLE: 6x + 3y + 9 = 0
                            3y = -6x - 9
                         3y/3 = -6x/3 - 9/3
                              y = -2x -3

We also learned how to do the opposite- rearranging an equation in slope y-intercept form to standard form.
To do this, we rearrange the terms to the left hand side of the equation, so it looks like this: Ax + By + C = 0
Then, on the right side, you just put a 0. Simple, right?

TIP: If the 'A' term is negative, divide all the terms by -1.
If there are fractions, then multiply each term by the lowest common denominator (LCD) to remove the fractions. 


EXAMPLE: y = 2x -5
    -2x + y + 5 = 0
   -2x/-1 + y/-1 + 5/-1 = 0
     2x - y - 5 = 0

Also, we learned about parallel and perpendicular lines. Parallel lines are lines that run in the same direction- they never cross!
For parallel lines, the slopes are equal. For example,
y = 3x + 5
y = 3x - 2

Perpendicular lines, on the other hand, are lines that intersect at right angles.
For perpendicular lines, the slopes are negative recriprocals.
EXAMPLE: 3/7 => -7/3
                   -2/3 => 3/2

Questions:
Rearrange the equation in standard form to slope y-intercept form.
1) 4x + 2y -6 =0

ANSWER: 2y = -4x + 6
                2y/2 = -4x/2 + 6/2
                     y = -2x + 3
2) 9x - 3y - 6 = 0

ANSWER: -3y = -9x + 6
              -3y/-3 = -9x/-3 + 6/-3
                      y = 3x -2

3) 8x - 4y + 16 = 0
                
ANSWER:  -4y = -8x - 16
              -4y/-4 = -8x/-4 - 16/-4
                      y = 2x - (-4)
                      y = 2x + 4

4) -12x + 2y - 18 = 0

ANSWER: 2y = 12x + 18
                2y/2 = 12x/2 + 18/2
                     y = 6x + 9
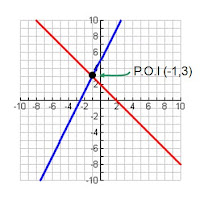Another thing we learned was linear systems. To solve linear systems, you need a POI, or point of intersection. Those points must satisfy the equation. An example is shown at the right.

-------------------------
Rearrange the equation in slope y-intercept form to standard form.

1) y = 3x - 6

ANSWER: -3x +y + 6 = 0
-3x/-3 + y/-3 + 6/-3 = 0/-3
               x + y/-3 -2 = 0

2) 3y = 6x + 12

ANSWER: -6x + 3y -12 = 0
    -6x/-6 + 3y/-6 - 12/-6 = 0/-6
           x + 3y/-6 - (-2) = 0
             x + 3y/-6 + 2 = 0

3) 2/3y = -1/6x + 4

ANSWER:  1/6x + 2/3y - 4 = 0
1/6x (6) + 2/3y (6) + 4 (6) = 0 (6)
                       x + 4y - 24 = 0

4) Real Life Scenario:

The grad committe is hosting a graduation party, and they are renting a hall at the Showcase Hall. The Showcase hall uses the equation 10n - C + 1300 = 0 to determine the cost for a hall rental.
C represents cost, in dollars
n represents the number of people attending the graduation party.

i) Rearrange the equation into slope y-intercept form.
10n - C + 1500 = 0
              -C = -10n - 1500
          -C/-1 = -10n/-1 - 1500/-1
                C = 10n + 1500
ii) What is the rental cost if 120 people attend the graduation party?
               C = 10n + 1500
               C = 10 (120) + 1500
               C = 1200 + 1500
               C = 2700
Therefore it would cost $2700 to rent the Showcase Hall for 120 people.

Labels: Lessons

Hello, my name is Sohyun Kim, and I am in grade 9. This site is for my math summative project, so no hateful comments please. I generally like to read, draw, read manga, and watch anime in my spare time.
Normal | Bold | Strikeout | Italic | Underline | Link | big | small

Polynomials: Algebraic expressions made up of terms
Monomial: 1 term
Binomial: 2 terms
Trinomial: 3 terms
Terms: Made up of a coefficient and variable(s)
Power: Product of identical factors and consists of 2 parts- exponent and base. Coefficient: ----
Variable: ----
Constant/constant term: A term with no variable
Hypothesis: A theory or statement that is either true or false
Statistics: The collection, organization, and analysis of numerical data
Primary Data: Data that comes from experiments and surveys done by researchers
Secondary Data: Data that already exists- comes from sources such as the internet, magazines, and Statistics Canada
Interpolation: Prediction involving a point within the set of data
Extrapolation: Prediction involving a point outside the set of data
Linear Relation: Relation between 2 variables, forms a straight line
Non-Linear Relation: Relation between 2 variables, does NOT form a straight line
Curve of best fit: Curve that comes closest to the points of a non-linear relation
First Differences: -----
Slope: The steepness of a line- ratio of the rise to the run between both points
Direct Variation: A relationship between 2 variables in which one variable is a constant multiple of the other
Partial Variation: When a relationship between 2 variables have both a fixed and variable amount
Continued -HERE-

Polynomials / Equations / Relations / Linear Relations / Analytic Geometry / Measurement / Helpful Tips /