In this unit, you will learn about the pythagorean theorem and the perimeter/area/surface area/volume of shapes and 3-D objects.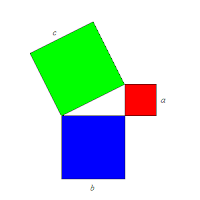 


First, there is the pythagorean theorem. 


The equation for the pythagorean theorem is a² + b² = c²
c^{² is the hypotenuse side.}


EXAMPLE:  Side a = 2 Side b = 8
What is the measure of side c?


a² + b² = c²
(2)² + (8)² = c²
      4 + 64 = c²
            68 = c²
                                                        68 squared = c² squared
                                                                   8.2  = c

    

Another thing we learned about is perimeter and area.
Here are the equations:


Rectangle
Perimeter: P= l + l + w + w   OR   P = 2 (l + w)
Area: A = lw


Parallelogram
Perimeter: P = b + b + c + c   OR   P = 2 (b + c)
Area: A = bh


Triangle
Perimeter: P = a + b + c 
Area: A = bh/2  OR   1/2bh


Trapezoid
Perimeter: P = a + b + c + d 
Area: A = (a + b)h /2   OR   1/2 (a + b)h


Circle
Circumference: C = πd    OR   2πr
Area: A = πr²


Cylinder
Surface Area: SA=2πr²+2πrh
Volume: V=πr²h


Sphere
Surface Area: SA=4πr²
Volume: V=4/3 πr³ 


Cone
Surface Area: SA=πrs+πr²
Volume: V=1/3 πr²h


Square base pyramidArea: A=2bs+b²
Volume: V=1/3 b²h


Rectangular prism
Area: A=2(wh+lw+lh)
Volume: V=lhw

Triangular prism
Area: A=ah+bh+ch+bl
Volume: V=1/2 blh


PRACTICE: 


1) 
What is the perimeter of this triangle?


ANSWER: P = 9 + 5 + 11 
                  P = 25


2) What is the area of a rectangle that has a length of 12m and a width of 4m?

ANSWER: A = lw
                  A = (12) (4)
                  A = 48m


3) Soda is sold in aluminum cans that measure 15cm in height and 6cm in diameter. What is the volume?


ANSWER: V=πr²h
                  V = (3.14)3² (15)
                  V = (3.14)9 (15)
                  V = 423.9 cm³
4)




Find the volume of this triangular prism.
V=1/2 blh
V= 1/2 (6.2) (4.3) (8.5)
V= 1/2 (226.61)
V= 113.30cm³

Another thing we learned about is the angle relationships in triangles.
The sum of the interior angles in a triangle is 180 degrees. Therefore, a + b + c = 180 degrees.
The sum of the exterior angles of a triangle is 360 degrees. Therefore, x + y + z = 360 degrees.
The exterior angle of each v ertex is equal to the sum of the two opposite interior angles, so x = b + c, y = a + c, and z = a + b. EAT (Exterior angle theorem)


A midpoint is a point that divides a line in half EQUALLY. 


TIP: the formula for the sum of the interior angles of a regular polygon is 180 (n-2)


In any quadrilateral, when you connect the midpoints of the sides, a parallelogram/rhombus is formed. 

Labels: Lessons

Hello, my name is Sohyun Kim, and I am in grade 9. This site is for my math summative project, so no hateful comments please. I generally like to read, draw, read manga, and watch anime in my spare time.
Normal | Bold | Strikeout | Italic | Underline | Link | big | small

Polynomials: Algebraic expressions made up of terms
Monomial: 1 term
Binomial: 2 terms
Trinomial: 3 terms
Terms: Made up of a coefficient and variable(s)
Power: Product of identical factors and consists of 2 parts- exponent and base. Coefficient: ----
Variable: ----
Constant/constant term: A term with no variable
Hypothesis: A theory or statement that is either true or false
Statistics: The collection, organization, and analysis of numerical data
Primary Data: Data that comes from experiments and surveys done by researchers
Secondary Data: Data that already exists- comes from sources such as the internet, magazines, and Statistics Canada
Interpolation: Prediction involving a point within the set of data
Extrapolation: Prediction involving a point outside the set of data
Linear Relation: Relation between 2 variables, forms a straight line
Non-Linear Relation: Relation between 2 variables, does NOT form a straight line
Curve of best fit: Curve that comes closest to the points of a non-linear relation
First Differences: -----
Slope: The steepness of a line- ratio of the rise to the run between both points
Direct Variation: A relationship between 2 variables in which one variable is a constant multiple of the other
Partial Variation: When a relationship between 2 variables have both a fixed and variable amount
Continued -HERE-

Polynomials / Equations / Relations / Linear Relations / Analytic Geometry / Measurement / Helpful Tips /